Why is it taking longer to get a Grab?

Or, less sexily, "On the scaling complexity of driver-rider matching through ridehailing platforms".

I live in Kuala Lumpur, Malaysia, where the simplest mode of transport for someone who doesn’t own a car (i.e. me) is to use a rideshare app (usually Grab). Recently, Grab seems to take longer and longer to assign me a driver - meanwhile, competitors to Grab have been popping up all around. We’ve had AirAsia Move coming up, Indrive moving in, and even Bolt expanding into the country.

This leads to the question - is Grab in trouble? Is this why getting a Grab is so slow and costly nowadays?

To understand this, let’s look at this in 4 sections:

• How does the number of required drivers scale with the demand?

• Does paying more help?

• How does the average waiting time evolve?

• What happens if we don’t have enough drivers?

How many drivers do we need?

Let’s start with a simple model: imagine a set of m drivers free to move on a flat plane. For simplicity, assume all drivers move at the same speed v. We can imagine all riders have the same upper limit which they are willing to wait for a driver, and so this imposes a maximum arrival distance. So let’s define a few parameters:

\(\begin {align*} l_p &= maximum \hspace{2mm} arrival \hspace{2mm} distance\\ A &= total \hspace{2mm} area \hspace{2mm} coverage \end{align*}\)

We are making the assumption that the maximum arrival distance is significantly smaller than whatever lengthscale the coverage area operates on, as presumably you’d rather a driver not come from the other end of the city. (Or, another country.)

Image source.

Let’s also assume the drivers are uniformly distributed throughout the city, which is not really representative of a real scenario, but serves well enough to generalize our dynamics. For a given point, the probability that x (< m) drivers are within range will be

(Probability of x drivers in range) * (probability remaining drivers are not) * (number of possible in-range driver combinations)

or

\(P(x) = \frac{m!}{x!(m-x)!}(\frac{\pi l_p^2}{A})^x(1-\frac{\pi l_p^2}{A})^{m-x}\)

And the probability at least one driver is in range of a rider is

\(\begin{align*} P( \geq 1) &= 1 - (1 - \frac{\pi l_p^2}{A})^m\\ &= m\frac{\pi l_p^2}{A} + \mathcal{O}(\frac{m l_p^2}{A})^2 \\ &\approx m\frac{\pi l_p^2}{A} \end{align*}\)

So what we see that, in a simple model, the number of drivers needed scales (predictably) as the maximum arrival distance squared. This means maximizing this arrival distance is necessary to cope with larger demand.

What about when there’s more than one rider in question? This is an exercise left to the reader. ¬‿¬

But really, in the simplest form it’s a sum of the binomial probabilities of at least n drivers being around (ignoring cases where a single driver is matched to more than one rider). You can possibly approximate this to a Poisson distribution with a large number of riders and drivers across a wide area.

Molkenthin et al. have a nice way of looking at scaling - we can directly define an effective scaling parameter x, where

\(\begin{align*} x &= \frac{\langle l \rangle \lambda}{vB} \\ \langle l \rangle &= average \hspace{2mm} travel \hspace{2mm} distance\\ \lambda &= request \hspace{2mm} rate\\ v &= average \hspace{2mm} vehicle \hspace{2mm} speed\\ B &= Fleet \hspace{2mm} size \end{align*}\)

Intuitively, this is a measure of

(How quickly am I getting new requests) / How quickly can I fulfill each request)

So if we have x > 1, you need a larger fleet size to cope with demand.

But what if we pay more? Does it help if we increase the prices to incentivize drivers from further out to pickup riders? This is especially relevant for heavier traffic, as is common when it rains - the occurrence of rain and the spike in Grab prices is now a well-known phenomenon. This is what we refer to as surge pricing.

Does surge pricing help?

To answer this, let’s try to first look at the fundamental idea behind surge pricing. Let’s create a simple mathematical model and define some parameters:

\(\begin{align*} E &= average \hspace{2mm} earnings\hspace{2mm}per\hspace{2mm}day\\ C &= earnings \hspace{2mm}per\hspace{2mm} km\\ N &= total\hspace{2mm}trips\hspace{2mm}per\hspace{2mm}day\\ v&=average\hspace{2mm}vehicle\hspace{2mm}speed\\ l_p &= average\hspace{2mm} distance\hspace{2mm} to \hspace{2mm}pickup\\ l_T &= average \hspace{2mm} distance\hspace{2mm}to\hspace{2mm}dropoff \end{align*}\)

Now each trip takes a total duration of

(the time it takes to reach the rider) + (the time to reach the destination)

i.e.

\(\tau = \frac{l_p+l_T}{v}\)

and the earnings for each trip is (the earnings per km) * (the distance you get paid for), i.e.

\(\bar{C} = l_T * C\)

Note that drivers do not get paid for the total trip distance (as far as I know), only the distance from the pickup to the dropoff point. Now you could argue distance to pickup does factor in a little through surge pricing, but in practice I don’t think it’s baked in explicitly to the algorithm.

The total number of trips each driver can make in a day, N, will be

(Total working hours) / (total time per trip),

i.e.

\(\begin{align*} N &= \frac{W}{\tau}\\ &= \frac{Wv}{l_p+l_T} \end{align*}\)

Where W is the working hours in a day. We also have that

\(\begin{align*} E &= N*C_T\\ &= N*C*l_T \end{align*}\)

Therefore we can get that

\(\begin{align*} \frac{E}{C*l_T} &= \frac{Wv}{l_p + l_T}\\ C &= \frac{E}{Wv}(\frac{l_P}{l_T} + 1 ) \end{align*}\)

i.e.:

• When the time the driver takes to reach the rider is small compared to the rest of the trip, then costs are largely dominated by driver earning expectations;

• When time to reach the rider is long, then the costs of the trip grow linearly with the arrival distance.

Therefore very simply, this linear relationship causes the associated cost increase - in addition, the sudden increase in arrival times with not enough drivers can lead to massive spikes in surge pricing. However the arrival time and dropoff time are not necessarily independent - presumably, a long arrival time is caused by traffic, and this will also affect time to dropoff. So let’s add a few more parameters:

\(\begin{align*} \tilde{C} &= time \hspace{2mm} cost \hspace{2mm}of \hspace{2mm}driver\\ C_{max} &= maximum \hspace{2mm} viable \hspace{2mm} cost \hspace{2mm} of \hspace{2mm} trip \end{align*}\)

What we can then say is that

\(\begin{align*} \frac{\tilde{C}(l_p+l_T)}{v} \leq C_{max}*l_T \end{align*}\)

which just says that a driver’s time cost for a trip cannot exceed the maximum cost a passenger is willing to pay for a trip (assuming such a value exists). So we can get that

\(\frac{C}{\tilde{C}} \geq \frac{1}{v} (\frac{l_p}{l_T}+1)\)

This is a pretty nice and intuitive relation IMO - it essentially says that the profit margin of a driver (and Grab) depends on how much time you spend getting paid (dropping off). So looking at this, we may make a few claims:

• When your pickup-dropoff distance is large, your drivers may be more willing to come in from farther as the profit margin offsets the time to get to the rider; however,

• when the distance to pickup is roughly comparable to the arrival-dropoff distance, the costs need to scale linearly.

Given that probability of finding a driver is proportional to (arrival distance) squared, what we can say is that

the cost increases scales as the root of the probability you find a driver.

This means that when you pay twice as much, you increase the likelihood of finding a driver by four times.

So how long do I need to wait >.<

Let’s call the probability you don’t get a driver by a given time t as S(t), which is commonly referred to as the “survival probability”. Therefore the rate at which a rider gets a driver, f(t), is given by how quickly this probability decreases, i.e.

\(f(t) = -\frac{dS}{dt}\)

and the average waiting time is given by

\(\langle T \rangle = \int_0^{\infty} tf(t) dt = \int_0^{\infty} S(t) dt \)

So how do we find S(t)? Let’s again assume drivers are uniformly distributed across the city. Taking a note from Qiang et al., let’s denote the number of drivers reaching the “acceptable pickup zone” at a rate R, then the probability of k drivers arriving by time t is a Poisson distribution

\(\begin{align*} P_k(t) &= \frac{(Rt)^k}{k!}e^{-Rt}\\ P_0(t) &= e^{-Rt} \end{align*}\)

Now the survival probability will just be the probability no drivers have reached till time t. While we can follow the formula above for f(t), we can also obtain it more fundamentally: the likelihood f(t) of a rider getting a ride at time t is

(the probability no drivers have reached till time t - dt) * (the probability a driver reaches the “acceptable pickup zone”) in time dt)

or

\(\begin{align*} f(t) &= P_0(t-dt) * (1-P_0(dt))\\ &\approx e^{-Rt} * (1-e^{-Rdt})\\ &= e^{-Rt} * (1-(1-Rdt+\mathcal{O}(dt^2)))\\ &\approx Re^{-Rt}dt \end{align*}\)

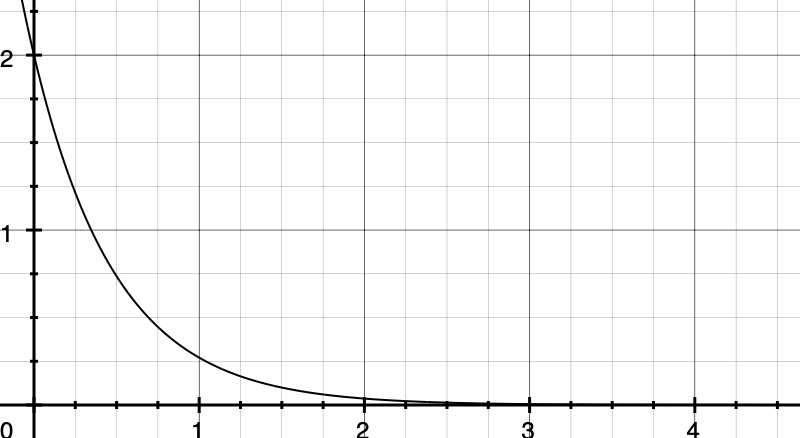
If we examine how this looks like on a graph, most rides would (thankfully) happen immediately after a booking.

The average waiting time will be

\(\begin{align*} \langle T \rangle &= \int_0^{\infty} tf(t) dt \\ &= \int_0^{\infty} e^{-Rt} dt \\ &= \frac{1}{R} \end{align*}\)

i.e. the average waiting time is inversely proportional to the rate at which drivers are reaching the average pickup zone. Using Molkenthin’s work as a basis, we can roughly get a timescale for R as

\(\begin{align*} R &\sim \frac{vB}{\langle l \rangle } \\ \langle T\rangle &\sim \frac{\langle l \rangle}{vB} \\ \langle l \rangle &\sim l_p \end{align*} \)

and so the waiting time scales inversely to the fleet size B and travel speed v, while being proportional to the average distance from the driver to the pickup point (ie. the “acceptable pickup radius”).

A few interesting things to note:

• For large fleet sizes, increasing the fleet size makes diminishing returns on waiting times: unless the demand outstrips how many drivers are available, at a large population of drivers the limiting factors instead become the travel speed and the distance to pickup.

• While increasing the acceptable pickup radius does increase the chance of matching with a driver, the pickup time still doesn’t change much - you can get matched early, but the driver still has to come to you.

• In that sense, you’re paying extra to get a driver, but you’re not necessarily reducing your waiting times.

Of course, this doesn’t account for the fact that drivers may decline a job.

But is it really a big deal if we don’t have enough drivers?

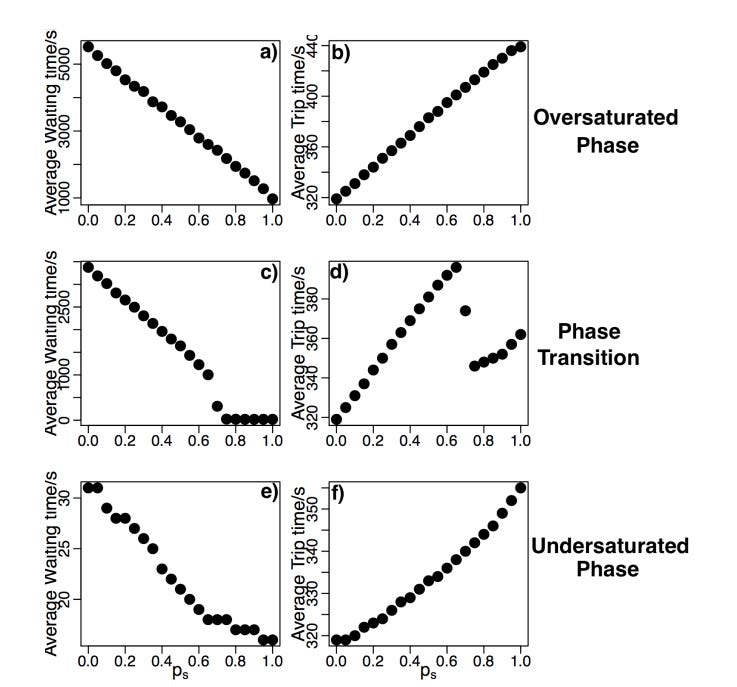
When you don’t have enough drivers, what’s interesting is that waiting time increases very quickly as found by Yang et al. This arises because of queue formation and accumulation - as requests build up, this causes a runaway effect.

At the phase transition between (having too many drivers) and (not having enough drivers), the waiting time increases sharply. Image and caption from Yang et al. (1)

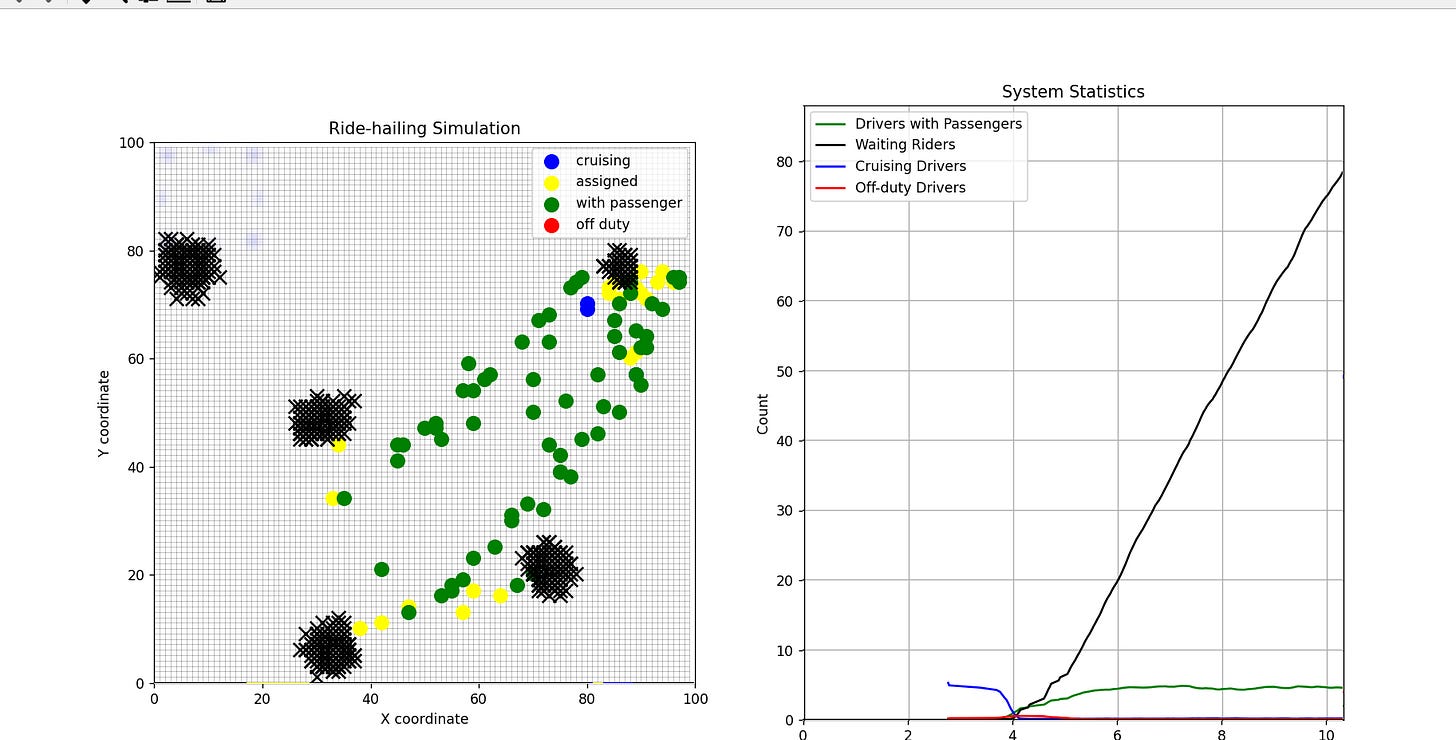
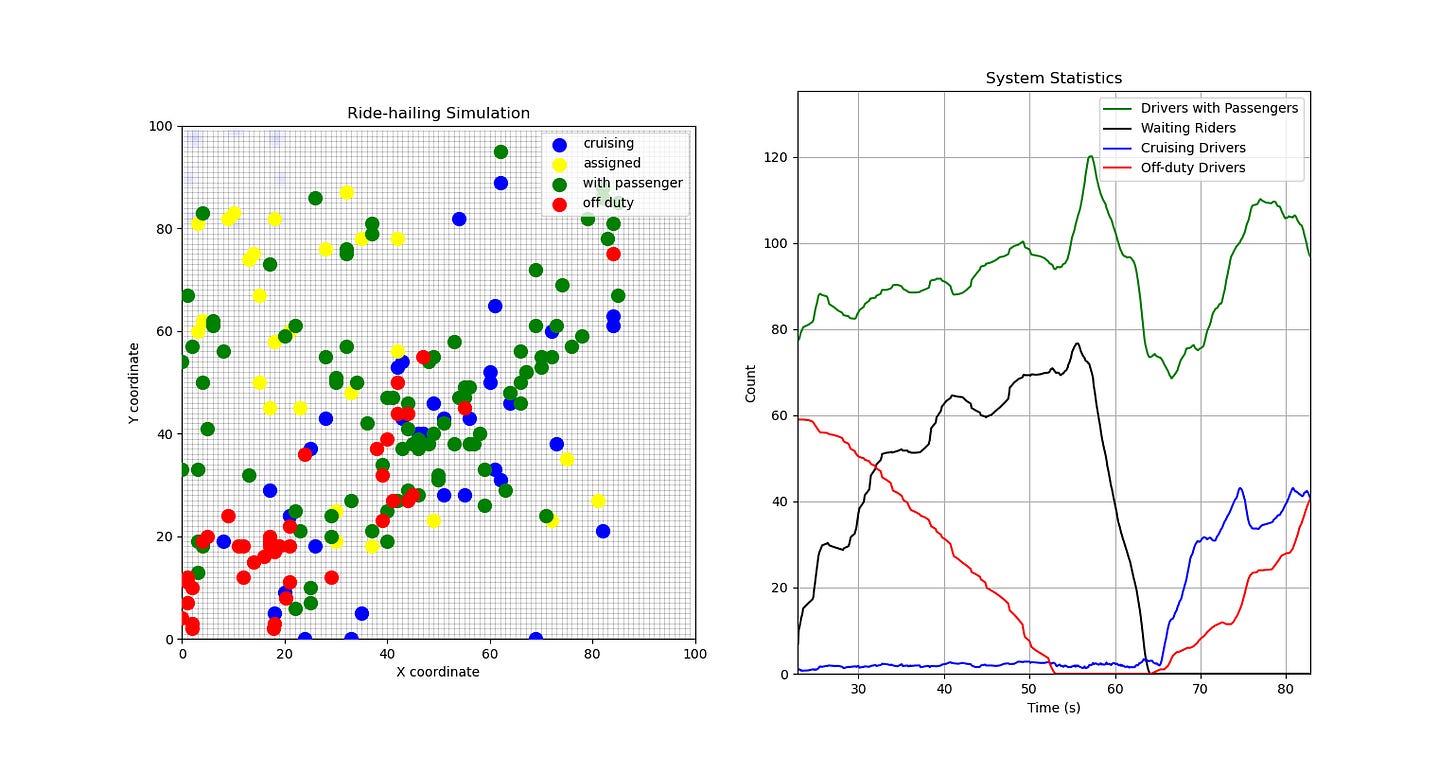
What’s interesting is that similar effects could be seen in some very simple simulations. Here’s a basic one I built in Python. (Or, more accurately, a basic one I asked Cursor to build for me.)

In this model, drivers can move around a flat grid, they pick up riders across the map, and drop them off at random locations. I’m generating riders in clusters across the map and also having riders spawn in a periodic pattern, to model how you may get rush hours. If there are too many drivers and not enough riders, then drivers start going off duty and “head home” (i.e. go to a corner of the map), but can also come back on if the demand exists.

What we see is that, if there are enough drivers to cope with peak demand, then everything is fine.

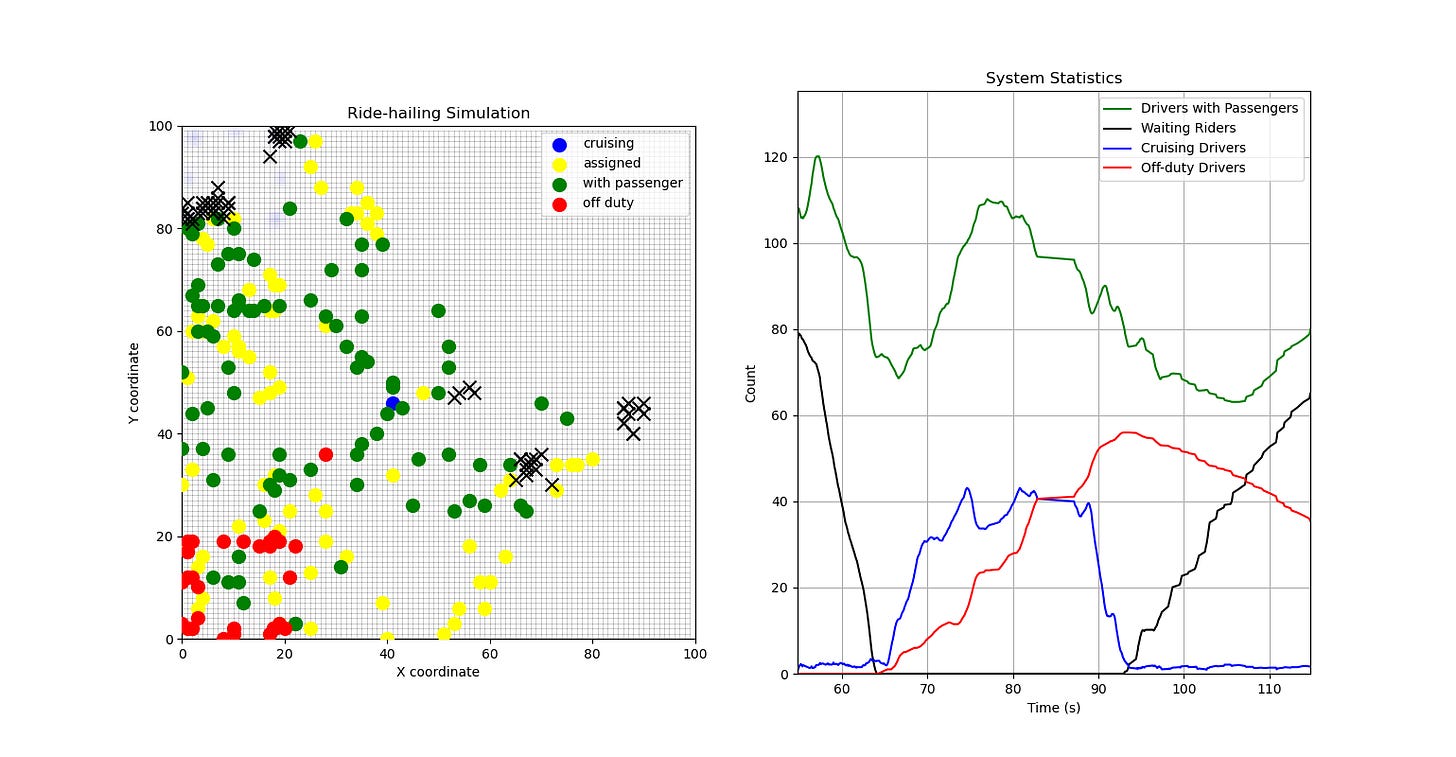
During peak times, the “reserve” of off-duty riders comes in to meet unmatched demand, and once demand starts to clear then drivers slowly move back to roaming the map or going off-duty.

Another illustration, just to demonstrate the demand cycles more clearly.

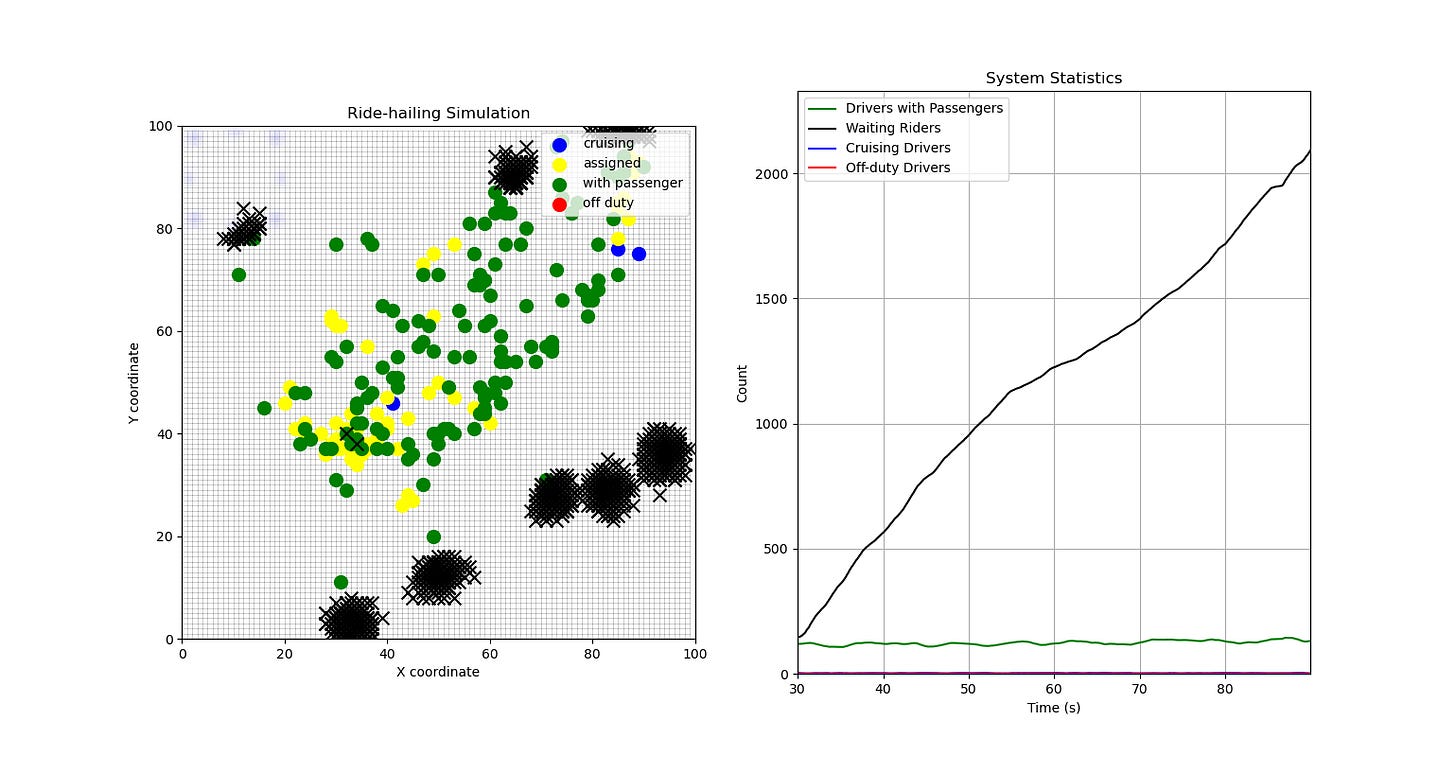
But if we can’t meet the peak demand quickly enough, then problems start to happen - queues start to form and you have all your drivers working all the time, but still not meeting the demand accumulation.

Now in practice queue formation may not be such a big issue, as presumably past a point your riders will simply give up on the platform and move somewhere else. But this is still not ideal because

• Poor customer experience leads to potential loss of a customer to another competitor platform, and

• your platform loses money.

On the other hand, what’s also interesting is to note that when there are sufficient taxis to meet demand, then increasing taxi number only provides marginal improvements to average travel time. As empty taxis are readily available, the marginal benefit of adding more taxis is limited to slightly reducing the average distance to a waiting passenger. This can also lead to an inefficient usage of drivers and/or lead to more disgruntled drivers leaving the platform due to lack of demand.

Ultimately, it’s a balance between

• having enough drivers on hand to cater for demand, and

• finding a way to retain drivers if not enough demand can be produced.

So what can be done about it?

Functionally a lot of this comes down to things outside Grab’s control,

• traffic,

• weather,

• public transport disruption,

• special events,

• road network connectivity,

• dinosaur attacks,

• etc.

However, there are some interesting ideas to look at. Molkenthin’s paper looks at scaling services through ridepooling, ie having one vehicle serve multiple customers at once. We may imagine a bus-on-demand model, such as what is being done here by Kumpool.

Image source: Kumpool

Of course, this comes with several caveats:

• In theory, matching and picking up on the way is a great idea to make efficient use of the bus. In practice, I wonder how long the travel time would be, especially if the bus has to stop every so often. This would slowly degrade back to the usual problems with public transport.

• You’re not actually increasing the probability of having a transport platform near you. This solves the cost problem but not necessarily the time-to-ride problem. Arguably there is some increase as you can have a larger pickup radius through offsetting the cost of a hire by spreading it more throughout the margins, but it’s not clear how large this is.

So what else? Will having more ride hailing platforms make things better? In my opinion, not necessarily - I’d expect the ride-hailing market in Malaysia to be nearing saturation (citation needed) so unless you’re drawing in more people to act as drivers, which is difficult, you’re not necessarily improving waiting times.

However, there is one thing that could be worth exploring - neighbourhood or community ride-hailing, instead of citywide ones. While a ride-hailing service that sends riders across the city is still necessary, we see that the largest change in waiting times happen when you add to small groups of drivers and reduce pickup distances. So if dropoff-pickup services could be locked to specific parts or neighbourhoods of the city, where both dropoff and pickup points happen in relatively small zones, and this were served by smaller communities - this could be a way to alleviate some of the demand issues faced on peak periods. There is also the option to explore ride-hailing through alternative modes of transport e.g. scooters and motorbikes, although I’m really not sure about the legalities - it seems like something Grab would already have taken from Gojek, if it were possible.

In summary…

• Things get really bad if you don’t have enough drivers. (Also if you have too many, but one is worse.)

• Paying twice as much increases the likelihood of you finding a driver by four times, but this doesn’t necessarily reduce your waiting time - just the likelihood of getting matched. So while surge pricing can be an effective and necessary component for driver-rider matching, you’re still restricted by waiting times for your driver to reach you.

• Consider a region-locked ridehailing service to supplement the main ridehailing service. If you can convince more regional drivers to come on board to a relatively small user pool and/or set a hard cap on the acceptable pickup distance to force a lower time to arrival, this could lower the transport times. You could also create a “chain” system for riders to hop around using a combination of several transport modes to lower costs and/or transport times.

Sources:

1. Yang, Bo & Ren, Shen & Legara, Erika Fille & Li, Zengxiang & Ong, Edward & Lin, Louis & Monterola, Christopher. (2018). Phase Transition in Taxi Dynamics and Impact of Ridesharing. Transportation Science. 54. 10.1287/trsc.2019.0915.

2. N. Molkenthin et al. Scaling Laws of Collective Ride-Sharing Dynamics. Phys. Rev. Lett. 125, 248302– Published 10 December, 2020

3. Xinwu Qian, Satish V. Ukkusuri. Taxi market equilibrium with third-party hailing service, Transportation Research Part B: Methodological, Volume 100, 2017

4. Method of Taxi Carpooling Probability and Wait Time Based on Poisson Distribution, XIAO Qiang, HE Rui-Chun, YU Jian-Ning, ZHANG Wei, MA Chang-Xi. China Journal of Highway and Transport ›› 2018, Vol. 31 ›› Issue (5) : 151-159.